Lecture 1. 선형 방정식의 기하학 (The geometry of linear equations)

다음은 Gilbert Strang의 선형대수학 MIT 강의를 듣고 정리한 글이다. 강의 링크

선형대수학의 기본문제 (Fundamental Problem)

연립 선형방정식 (System of Linear Equations)을 푸는 것이다.

연립 선형방정식의 풀이

풀이에 앞서, 미리 알아야 하는 개념들이 있다.
연립 선형방정식은 두 가지 방법으로 표현될 수 있는데, Row Picture와 Column Picture (중요!) 가 그것이다.

아래의 예시를 통해 비교해 보겠다.
$$ 2x -y = 0 \\ -x + 2y = 3 $$

다음을 Row Picture 방식으로 표현해 본다면
$$
\begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix}
\begin{bmatrix} x \\ y \end{bmatrix} =
\begin{bmatrix} 0 \\ 3 \end{bmatrix} (Ax=b \text{ 꼴})
$$
A는 계수 행렬 (Coefficient Matrix), x는 미지수로 이루어진 벡터, b 역시 벡터이다.
(앞으로 각 위치의 행렬을 A, x, b 로 설명할 것이다.)

이를 좌표계로 옮겨서 표현한다면 다음과 같이 표현할 수 있다.

Row Picture

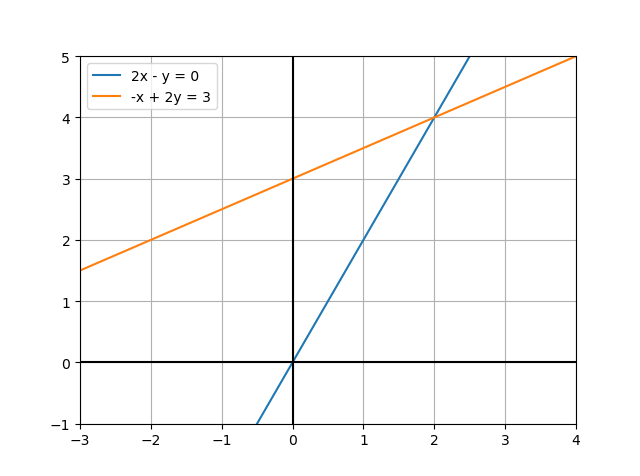
만약 Column Picture 방식으로 표현한다면, 다음과 같이 표현할 수 있다.
$$
x \begin{bmatrix} 2 \\ -1 \end{bmatrix} +
y \begin{bmatrix} -1 \\ 2 \end{bmatrix} =
\begin{bmatrix} 0 \\ 3 \end{bmatrix}
$$
이 방정식이 의미하는 바는 왼쪽의 벡터([2, -1])과 오른쪽의 벡터([-1, 2])를 올바른 양으로 결합하여 b를 구하라는 것이다.
이는 곧 올바른 조합을 찾으라는 것이고, 이것을 선형 결합 (Linear Combination) 이라고 한다.

예시에서는 왼쪽 벡터 1개, 오른쪽 벡터 2개를 결합함으로써 b를 얻을 수 있다.

Column Picture

만약 두 벡터의 모든 선형 결합들을 찾는다면 어떻게 될까? 그 결과는 2차원 공간을 모두 채울 수 있을 것이다.

3차원의 경우에도 마찬가지의 결과를 얻을 수 있다.
다음의 예시로 진행을 해 볼 것이다.

$$
2x -y = 0 \\
-x + 2y - z = -1 \\
-3y + 4z = 4
$$
예시를 Row Picture와 Column Picture로 나타내 보면 다음과 같다.

$$
\begin{bmatrix} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -3 & 4 \end{bmatrix}
\begin{bmatrix} x \\ y \\ z \end{bmatrix} =
\begin{bmatrix} 0 \\ -1 \\ 4 \end{bmatrix} \text{ or} \\ \text{ } \\
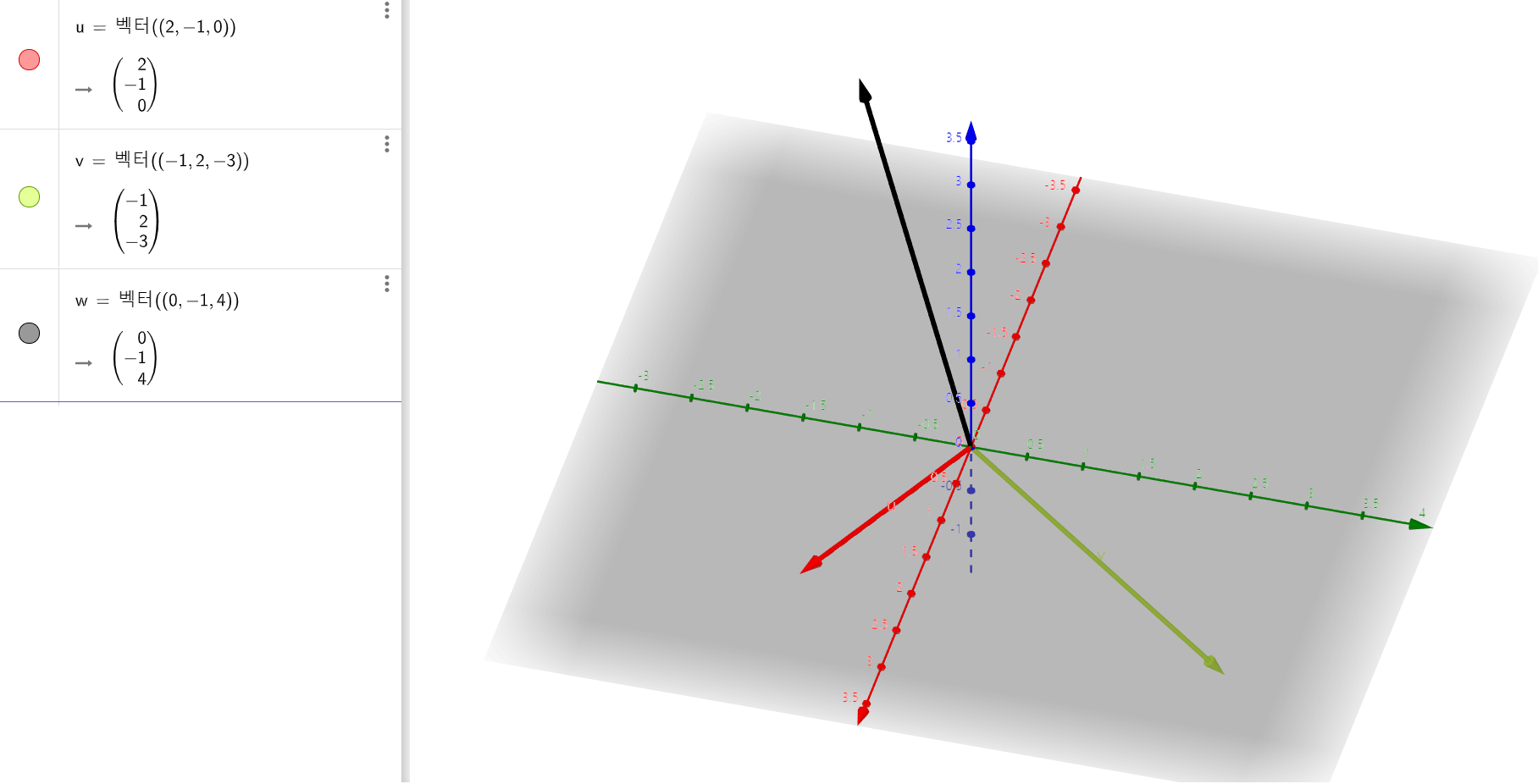
x \begin{bmatrix} 2 \\ -1 \\ 0 \end{bmatrix} +
y \begin{bmatrix} -1 \\ 2 \\ -3 \end{bmatrix} +
z \begin{bmatrix} 0 \\ -1 \\ 4 \end{bmatrix} =
\begin{bmatrix} 0 \\ -1 \\ 4 \end{bmatrix}
$$

3차원 그래프

Row Picture

Column Picture

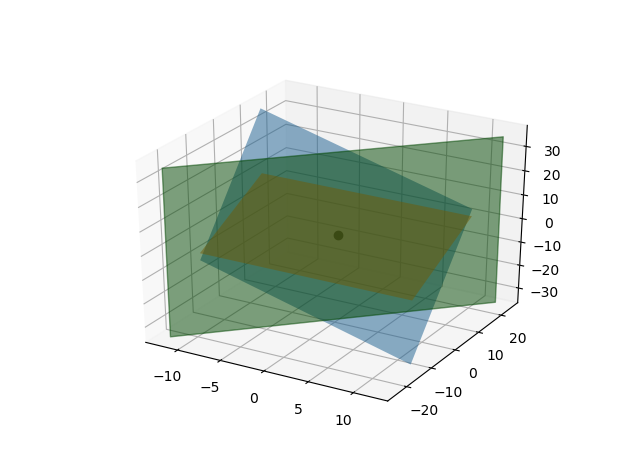
이제 고려해야 할 문제는 b에 어떤 값의 벡터가 들어가더라도 해를 구할 수 있는가? (Can I solve Ax=b for every b?)
다시 말해서, Column Vector들의 선형 결합으로 해당 공간 상의 모든 b를 만들어 낼 수 있는가? ( Do the linear combinations of the columns fill N-Dimension? )

위 3차원 연립방정식 예제에 대해서 답은 "YES"이다. 그리고 답이 "YES"라면 행렬 A를 가역행렬 (Invertible Matrix, Non-singular Matrix) 이라고 한다.
만약 답이 "NO"라면 행렬 A는 Singular Matrix가 된다.
Singular Matrix가 되는 경우의 예시를 들면 세 벡터가 모두 한 평면에 놓여있을 때가 될 것이다. 다시 말해 한 벡터가 다른 두 벡터의 선형 결합으로 표현될 수 있을 때를 의미한다(이를 linearly dependent라고 한다).
이런 상황에선 b가 평면 위의 벡터라면 나타낼 수 있겠지만, 평면 밖으로 벗어나면 b를 만들어 낼 수 없게 된다.

이 아이디어는 3차원, 4차원, 그 이상의 차원으로 진행시켜도 마찬가지의 결과를 얻을 수 있다.